2021

PID szabályzó teszt

A projekt célja: A PID szabályzókról megszerzett elméleti tudásom bővítése és kipróbálása a gyakorlatban, a mélyebb megértés céljából.

Néhány kép a projektről:

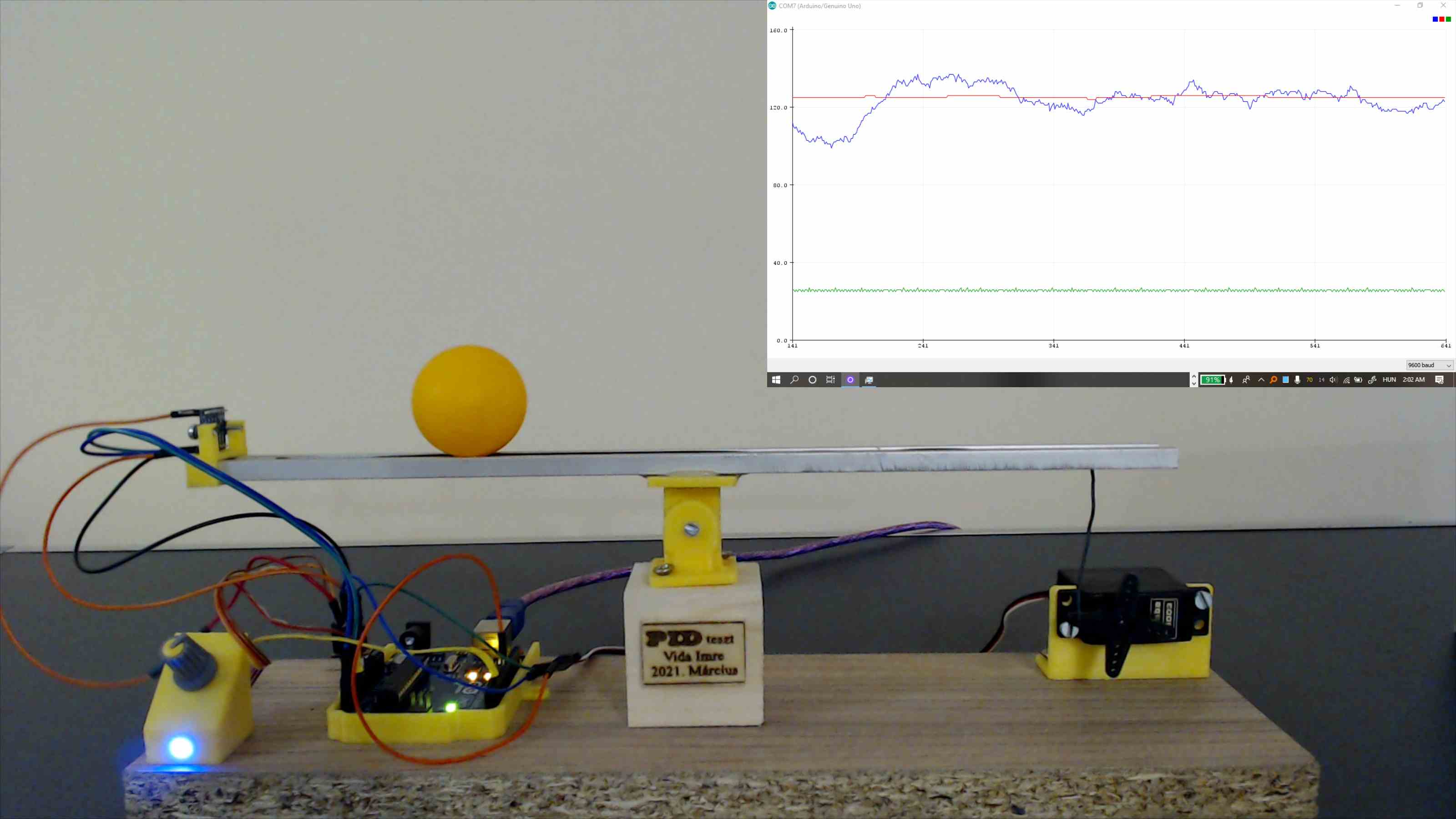
Folyamatban lévő projekt, hibák előfordulhatnak és a tartalom változhat.
Minden jog fenntartva! All rights reserved!

Összefoglalás:

Hardver:

A rendszer néhány alapvető elemből épül fel, melyek bárki számára könnyen beszerezhetők.

Felhasznált alkatrészek:

• Szervo motor
• Arduino Uno
• VL53L0X alapú ToF lézeres távolságmérő modul
• 1kΩ-os lineáris potméter
• LED + 270Ω-os előtét ellenállás


• Kis méretű MDF lap és egy fa kocka a mozgó szerkezet megemelésére.
• Lapos alumínium profil, és azon könnyen gördülő golyó (én egy ping-pong labdát használtam)
• Vezetékek, csavarok és alapvető eszközök az összeszereléshez
• 3D nyomtatott alkatrészek ( Stl fájlok letölthetők innen. )
  • Szenzor rögzítő
  • Szervo tartó elem
  • Rúd rögzítő elem
  • Rögzítés a mikrokontrollernek
  • Potméter és LED tartó kezelőpanel

Működési elv, és matematikai háttér:

A szabályzó célja, hogy a mozgatható rúd tetején lévő labdát a beállított pozícióban tartsa. A rendszer bemenete a szervo motor szöge, ezt lehet befolyásolni a mikrokontrollerrel. A kimenet a labda távolsága a távolságmérő szenzortól.

A rendszer átviteli függvényét az alábbi módszerrel számoltam ki:
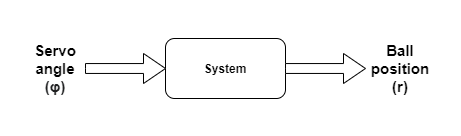
Első lépésként felvettem a számításhoz szükséges adatokat és elneveztem a változó mennyiségeket az alábbi ábra szerint.

Első lépésként azt számoltam ki, hogy a szervo ϕ szögváltozás hatására milyen magasságba képes emelni a középen rögzített alumínium rúd egyik oldalát. Ezt az alábbi összefüggés írja le. A számításokat az SI mértékegységekhez igazítottam. $$x=\sin \left(φ\right)\cdot \frac{15}{1000}$$ Ennek segítségével adódik, hogy a motor szögének változása hogyan hat a rúd szögére. $$α=\arcsin \left(\frac{\sin \left(φ\right)\cdot \frac{15}{1000}}{\frac{140}{1000}}\right)$$ Látható, hogy ez egy nemlineáris összefüggés ami nagy mértékben bonyolítja a későbbi számításokat. A motor által beállítható szögeket behelyettesítve, és ábrázolva belátható, hogy a működési tartományon belül az összefüggés jó közelítéssel tekinthető lineárisnak. A linearizáláshoz a ϕ=±60°-os szöget használtam. Ezután a függvénykapcsolat felírható m*ϕ alakban, ahol m a linearizálás közben kiszámolt meredekség.

A korábbiak ismeretében felírható a labda gyorsulása: $$a=g\cdot \sin \left(α\right)=g\cdot \sin \left(m\cdot \:φ\right)$$ Ezen a ponton az időtartománybeli vizsgálatból áttérhetünk a komplex-frekvenciatartományba, és a fenti egyenlet Laplace transzformáltját kétszer megszorozva (1/s)-el megkapjuk a gyorsulás függvény második integráltjának (az elmozdulás függvénynek) Laplace transzformáltját.
Az átviteli függvény ebből átrendezve a következő alakban írható fel: $$Wsystem(s)=\frac{7.875e17 s^2}{4.504e17 s^4 + 1.431e16 s^2}$$ Ez a folytonos rendszer átviteli függvénye. Mivel a szabályzó mintavételes rendszerhez lesz alkalmazva, számolni kell a mintavételek közti holtidővel, ami a fázistartalékot is rontani fogja. A maximális holtidőt jelen esetben 27ms-nak választottam, ennyi időbe minden esetben belefér a ToF szenzor egy mérése, a mérés utáni számítások és a grafikon megjelenítés céljából a kommunikáció lebonyolítása a soros interfészen.
A holtidővel korrigált átviteli függvény a következő: $$Wsystem(s)=e^{-0.027\cdot \:s}\cdot \frac{7.875e17s^2}{4.504e17s^4+1.431e16s^2}$$ A cél, hogy a labdát a megfelelő pozícióban tartsa a vezérlő, úgy hogy a fizikai rendszerbe a szervo motor szögének állításával tud beavatkozni. A szabályozási feladatra egy visszacsatolt soros kompenzátort választottam a PID szabályzót. A szabályozási kör a következőképp néz ki a külső zajokat, mérési és kvantálási hibákat figyelmen kívül hagyva:
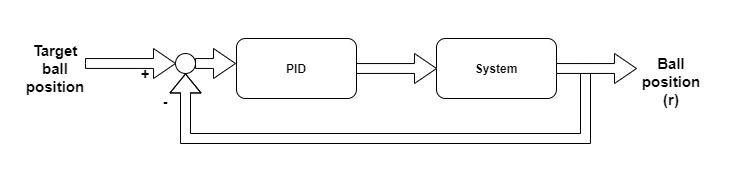
A PID szabályzó általános egyenlete: $$u\left(t\right)=K_p\cdot e\left(t\right)+Ki\cdot \int _0^te\left(t'\right)dt'\:+\:K_d\cdot \frac{de\left(t\right)}{dt}\:$$ Ahol Ki, Kd és Kp hangolható együtthatók.
A felnyitott kör átviteli függvényének Bode diagrammja a következő, jelölve rajta a közel 60°-os fázistartalékot, ami a tervezési cél. Ekkora fázistartalék esetén a figyelmen kívül hagyott "kicsi" hibák, nagyon kis valószínűséggel teszik instabillá a rendszert.

A tervezési szempontjaimnak eleget tevő, behangolt szabályzó együtthatói:

• Kp = 0.3949
• Ki = 0.0082
• Kd = 10.8231

A mikrokontrolleren futó program forráskódja elérhető a GitHub-on az alábbi linken: PID_ball_test

Végeredmény:

További elemzés:

Bár az alkalmazott PID szabályzó megfelelő alapjelkövetést biztosít az integrátor miatt 0 maradó hibával, a zavar-elnyomása lassú. Ez annak köszönhető, hogy a rendszer bemenete és a kimenete közötti átvitel optimalizálása volt a cél, cserébe a fizikai szakasz bemenetére érkező zavarás és a kimenet közötti átvitel tranziense jelentősen lelassult. Jelen esetben az ilyen zavarást úgy modellezhetnénk, hogy az eszköz egyik oldalát az alapjánál fogva megemeljük, és egy magasabb pontra helyezzük.

A jelenlegi szabályzó zavarás-elnyomása, valamint zavarás-kimenet ugrásválasza az alábbi ábrákon tekinthető meg:

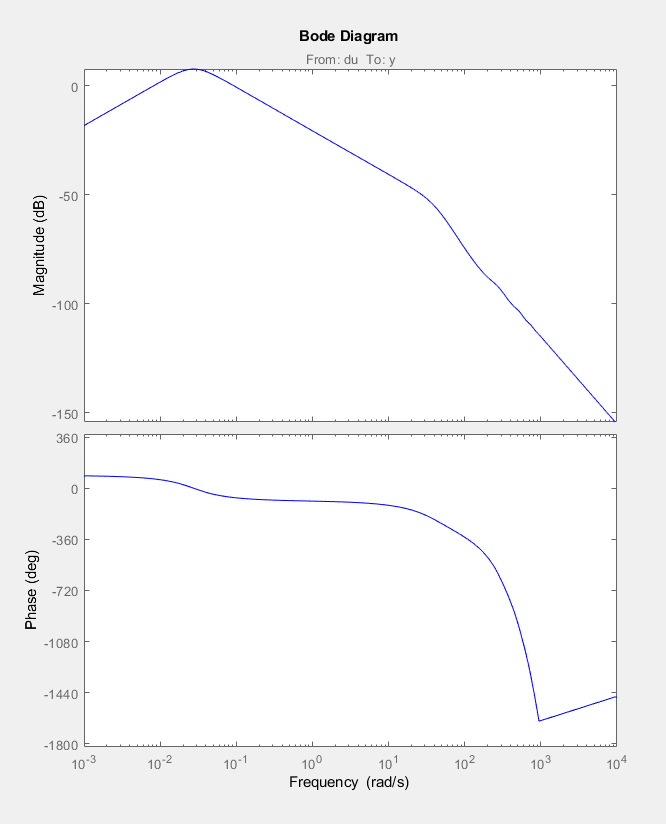
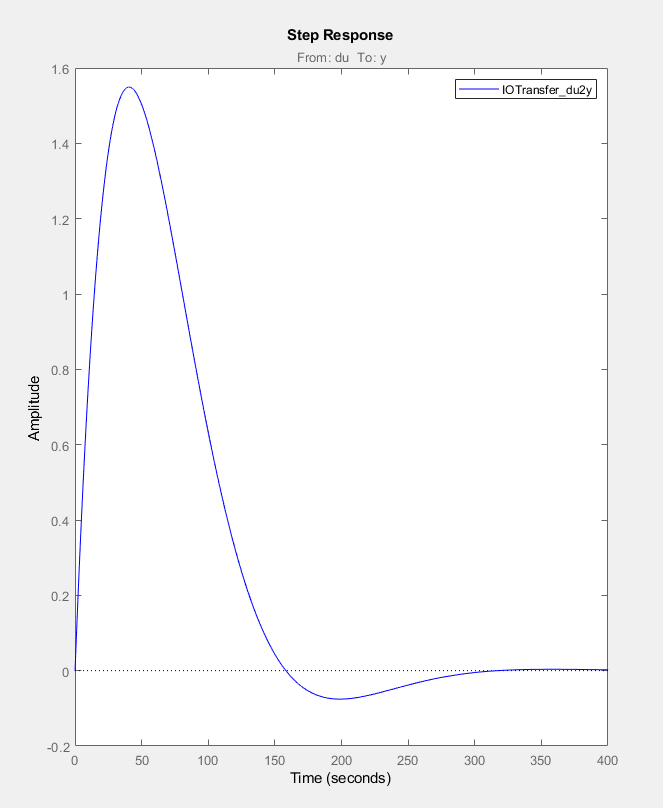
Erre megoldást egy 2 szabadsági fokkal rendelkező szabályzó jelenthet. Részletek hamarosan.

Pályázatok és versenyek:

• 2021. Budapesti Műszaki és Gazdaságtudományi Egyetem Kütyüpályázat 3. helyezés
• 2022. A működő eszköz jelenleg a Budapesti Műszaki és Gazdaságtudományi Egyetem I épületében van kiállítva.